QuickSort

Type: Divide and Conquer algorithm (Divide et Impera)
Created by: Sir Charles Antony Richard Hoare in 1962
Complexity:

• a worst-case running time \displaystyle O(n^2)
• an expected running time \displaystyle O({n}log{n})

Stability: not stable

Basic principle

Algorithm picks an element called pivot and rearranges the given array around the chosen pivot. Every manipulation is done within one array without creating any additional helping arrays.

Divide

The “Divide” part of the algorithm is achieved by a function called partition. Partition is a process of rearranging the initial array into two subarrays using the following logic:

• each element in the first subarray must be less than or equal to the pivot
• each element in the second subarray must be greater than the pivot

Return value is an index of the pivot in the entire array between the two subarrays.

Conquer

The “Conquer” part of the algorithm: sort the subarrays by a recursive calling of the quicksort.

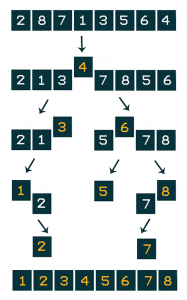
Example

Let’s say that we choose the last element of the array and its subbarrays as pivot (yellow color). By partitioning we can find the right place of the pivot in the array.

1.In the 1 iteration we have:

• 4 is pivot
• 2, 1, 3 are less than the pivot
• 7, 8, 5, 6 are greater than the pivot
• after defining which values are greater than 4 and which are less we have to place the pivot on the right place in the array. The index of the value 4 after partitioning will be index[3].

2.Call the quicksort on the subbarrays.

Methods to choose a pivot

• first element – always pick up the first element as pivot
• last element – always pick up the last element as pivot
• median element – always pick up a median element as pivot
• random sampling – select a randomly chosen element from the subarray as pivot

Complexity

• a worst-case running time \displaystyle O(n^2)
• an expected running time \displaystyle O({n}log{n})

Efficiency of the quicksort depends on the choosing of the pivot.

Imagine, we have an already sorted array in the descending order and we choose the right element as pivot.

100   97  76  55  43  28  12

All elements are less than the pivot and there are no elements greater than the pivot. After calling the quicksort in the first iteration we will get:

97  76  55  43  28  12  100  

The same will happen with all subbarrays.

97  76  55  43  28  12  100

76  55  43  28  12  97 100

In the above described case the array will be splitted n times and elements will be swapped n times which leads to the complexity of a worst-case running time \displaystyle O(n^2).

To make the above example better complexity, a pivot from the middle of the array should have been chosen. If a pivot is chosen ideally then after each recursive calling of the quicksort, an array will be splitted by \displaystyle O(log{n}) number of callings. Within each such recursive calling n elements will be swapped. That gives \displaystyle O({n}log{n}) complexity.

If we choose an improper pivot then an array will not be splitted and the problem will not be devided on subproblems. In this case we will just put pivot on its right place. For each calling of the quicksort we will need n operations to put pivot on its right place. That leads to \displaystyle O(n^2) complexity.

Implementation

Recursive on Python:

 
def quicksort(array, left, right):
    if (left < right):
        index = partition(array, left, right)
        quicksort(array, left, index - 1)
        quicksort(array, index + 1, right)


def partition(array, left, right):
    pivot = array[right]
    boundary = left - 1
    for j in range(left, right):
        if array[j] <= pivot:
            boundary += 1
            swap(array, boundary, j)
    swap(array, boundary + 1, right)
    return boundary + 1


def swap(array, i, j):
    array[i], array[j] = array[j], array[i]


if __name__ == "__main__":
    array = [2, 8, 7, 1, 3, 5, 6, 4]
    quicksort(array, 0, len(array) - 1);
    print(array)

Iterative on Python:

 
def quicksort(array, left, right):
    stack = list()
    stack.append(left)
    stack.append(right)

    while (stack):
        right = stack.pop()
        left = stack.pop()

        index = partition(array, left, right)

        if (index - 1 > left):
            stack.append(left)
            stack.append(index - 1)

        if (index + 1 < right):
            stack.append(index + 1)
            stack.append(right)


def partition(array, left, right):
    pivot = array[right]
    boundary = left - 1

    for j in range(left, right):
        if array[j] <= pivot:
            boundary += 1
            swap(array, boundary, j)
    swap(array, boundary + 1, right)
    return boundary + 1


def swap(array, i, j):
    array[i], array[j] = array[j], array[i]


if __name__ == "__main__":
    array = [8, 3, 6, 4, 1, 4, 2, 4, 150, 0, -1]
    quicksort(array, 0, len(array) - 1);
    print(array)